On 31st January 2018, Australia has a box seat for a Total Lunar Eclipse, where the Moon passes through the shadow (or umbra) cast by Earth. For the Eastern and Central States, and Northern Western Australia, the entire eclipse will be visible from start to finish. As a bonus, the dramatic full eclipse begins at the reasonably civilised hour of 12:00 AM AEDT.
On the West coast (including Perth), the initial phases of the eclipse won’t be visible, as the Moon will be below the horizon. However, within an hour of moonrise, with the Moon’s apparent size enlarged by being close to the horizon, the gradual reddening of the Moon towards the full eclipse at 8:50 pm will be an amazing sight.
As if that weren’t enough, there will be another Total Lunar Eclipse visible across Australia later in 2018 on the 27/28th of July.
So why the sudden silly season for eclipses? Why don’t we get them every Full Moon, where the Sun, Earth and Moon appear to form a straight line (known by the vowelless term syzygy).
Eclipse Anatomy
The fundamental reason for this is that the Moon DOES NOT orbit the Earth in the same plane in which the Earth orbits the Sun; it is actually inclined by close to 5.2 degrees. The direction of its inclination also changes as the Earth orbits the Sun: at some points, the inclination is directed towards or away from the Sun, at other points, it’s directed at right angles to the Sun. This geometry and the corresponding effect this has on eclipses is beautifully illustrated below:
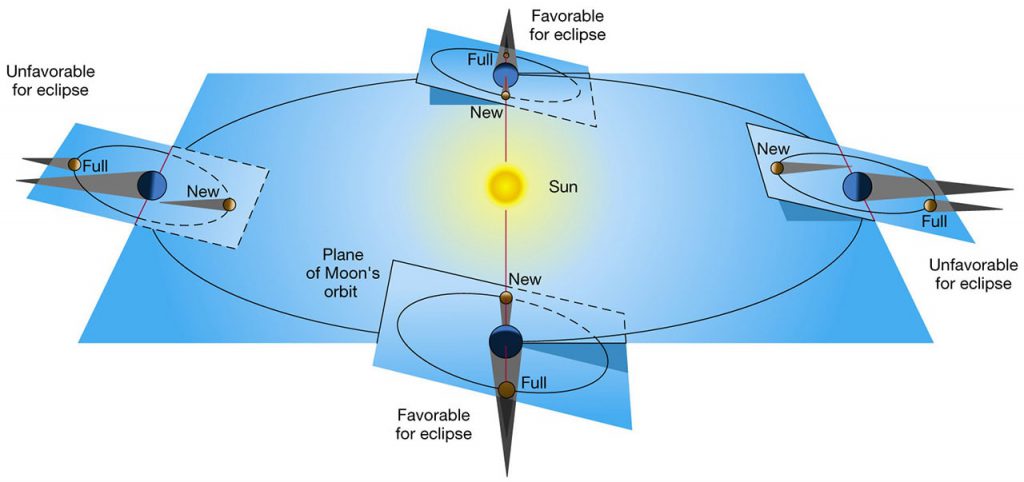
As can be seen, the favourable period for eclipses occurs twice per year when the inclination of the Moon’s orbit is at right angles to the Earth-Sun. These favourable points where the Moon crosses the Earth-Sun plane in line with the Earth and Sun are called nodes. However, to have a lunar eclipse, the Moon has to be at the node i.e. when it is full.
Scaling the Syszygy
Most diagrams and models in Astronomy (including the one in this article) are frustratingly labelled “Not to Scale”, generally due to the enormous disparities in sizes and distances involved. However, for the Sun-Earth-Moon system, we can scale things down to everyday objects to gain an appreciation as to why lunar eclipses do not occur every full moon.
For example, if we take the Earth as being a basketball, the Moon, with a diameter about one-quarter that of Earth, would then be very close to the size of a tennis ball. The distance between Earth and the Moon would on this scale be on average about seven and a quarter metres, plus or minus about 40 centimetres to account for the elliptical shape of the orbit. If we want to include the Sun, we would need a ball about 26 metres high; about the height of a seven-storey building. This ball would then need to be close to 3 kilometres away from the basketball to show the Earth-Sun distance. In one of the great coincidences of nature, at this distance, the Sun would appear to be the same size as our tennis ball moon. To simulate the Earth orbiting the Sun would require a near 18km walk around our scale model Sun!
Now as mentioned, the plane of the Moon’s orbit around the Earth is inclined about 5.2 degrees to the plane of the Earth’s orbit around the Sun. This translates to the Moon being up to 60 cm above or below the Earth’s orbital plane in our scale. The umbra of the Earth at the distance of the Moon would be a disc about 9 cm in radius, so it can be seen that the Moon has to hit a small target to become totally eclipsed.