How we figured out the speed of light
On the 7th December 2016, a Google Doodle appeared on Google’s search page. It depicted an extravagantly wigged man peering through a telescope as a pendulum clock ticked nearby. The man then walked away from his telescope apparently trying to understand what he had observed. The Google logo had been altered with a diagram showing the Sun, Earth, Jupiter and its innermost Galilean moon Io.

A few clicks revealed that the occasion was the 340th anniversary of a brief publication in Journal des Sçavans (Journal of Scientists) by the Danish astronomer Ole Rømer regarding his observations of Jupiter’s innermost Galilean moon Io, which strongly suggested that not only that light travelled at a finite speed, but also provided a remarkably accurate estimate of what that speed was.
Moon Clock
Rømer’s observations of Io were not initially for the purpose of determining the speed of light. It was in fact for the more practical reason of determining longitude, one of the most pressing problems of the era. The quest by John Harrison to construct an accurate clock whose accuracy would be unaffected by a ship’s motion is widely recounted. However, there were also attempts to use astronomical methods to determine longitude. One of these methods, originally proposed by Galileo, was to use the timings of when Io passes into and out of Jupiter’s shadow (which Rømer referred to as “immersions” and “emergences”); that is the timings of Jupiter-Io eclipses.
Io completes one orbit of the gas giant every 42.5 hours. If the times of its immersion into and emergence from Jupiter’s shadow could be accurately determined, then Io could be used as a clock to effectively give the local time at Greenwich. After determining the local time from solar noon, the longitude could be determined. Although this method of using Io’s eclipses proved impractical at sea, it could still be used on land.
The Speed of Light
We actually only have a vague outline of Rømer’s work in measuring the eclipses of Io at the Uraniborg and Paris Observatories, as the Copenhagen Fire of 1728 destroyed many of his records. In addition, the article in which he stated his results was very short (about 2 pages), and contained no details about his methods and observations. Some of his measurements have been subsequently found in correspondence, but debate continues as to the accuracy of his results (for example, see Shea (1998)).
In any case, Rømer convinced himself and many of his contemporaries (including Christian Huygens and Isaac Newton, though not his colleague Cassini) that he had measured a gradual change in the orbital period of Io. Specifically, he claimed there was a decrease in the orbital period of Io as Earth moved from the first quadrature (i.e. from where the Earth, Sun and Jupiter make a 90 degree angle) to opposition (i.e. Earth’s closest approach to Jupiter during its orbit). Then, as the Earth moved away from opposition to the second quadrature, the orbital period was observed to increase again. In terms of a clock, this is equivalent to the clock gaining time from opposition to conjunction, and then losing the same amount of time from conjunction back to opposition. Using modern data, the peak time gain should be about 16.5 minutes. This is shown in the graph below.
It was Rømer’s explanation of these phenomena that was the most important part. The diagram in the Google logo is based on the diagram Rømer included in his article to illustrate his hypothesis. The original diagram is shown below. Rømer suggested that during one orbit of Io when Earth is heading towards opposition H from quadrature at F, the Earth moves from F to G, thus shortening the distance between Earth and Jupiter during Io’s orbit. If we assume that light travels at a finite speed, the apparent orbital period of Io (measured by “immersions”) will appear less than if the Earth stayed in the same place F. Then, as Earth moves from L to K during one Io orbit away from the opposition, the distance between Earth and Jupiter increases, thus making the apparent orbital period of Io (measured by “emergences”) appear greater. Note that at opposition H, the Earth-Jupiter distance changes very little, so the orbital period of Io will not appear to change at H.
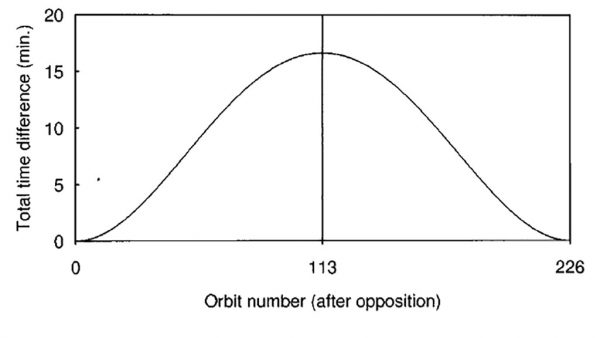
Graph showing how the cumulative gain in Io’s orbital period from opposition to opposition (Shea 1998). At its peak near conjunction, the Io “clock” has gained about 16.5 minutes, before losing the same time back at the opposition.
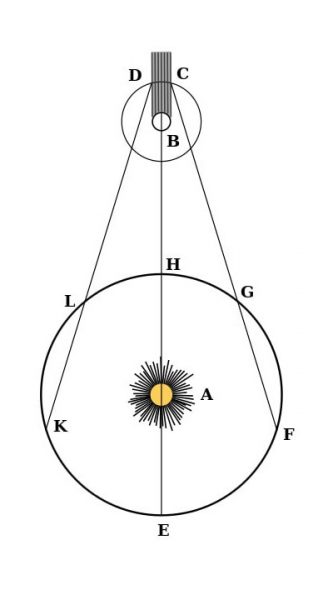
Left: The original diagram Rømer provided in the original article to illustrate his hypothesis to explain the apparent change in the orbital period of Io. A is the Sun, B is Jupiter. EFGHLK is the Earth’s orbit. The point F is the “first quadrature”, H is opposition, K is the “second quadrature” and E is a conjunction.
What Rømer had explained is a phenomena we now call the Doppler shift, where the apparent frequency or period of a physical process (e.g. sound waves) changes as we move towards or away from the source. In fact, a case could be made that the Doppler Effect should be renamed the Rømer Effect, as Christian Doppler didn’t provide his explanation until 1852.
Interestingly, Rømer did not explicitly calculate the speed of light based on his measurements. His only quantitative statement was that during the 42.5 hour orbit of Io, the Earth moved at least “210 Earth diameters.” Rømer’s famous contemporary, Christian Huygens, used Rømer’s data and method and arrived at the answer of 220,000 km/s in modern units, or about 26% lower than the current (exact) value of 299,792 km/s. This error is mainly due to the fact that the dimensions of the solar system were not known with great accuracy at that time.
Despite the issues around Rømer’s measurements, there is no doubt his paper contains a valid method for measuring the speed of light. Based on the solar system dimensions at the time, the first estimate of the speed of light using his method was of the right order of magnitude and thus allowed later scientists such as Hippolyte Fizeau and Albert Michelson to design terrestrial-based experiments to improve the accuracy of measurements of the speed of light.
References
Shea, James H. 1998. “Ole Rømer, the Speed of Light, the Apparent Period of Io, the Doppler Effect, and the Dynamics of Earth and Jupiter.” Am. J. Phys. 66 (7): 561-569.
Appendix: Rømer in his Own Words
Following is Rømer’s original explanation of his hypothesis from the Journal des Sçavans (Journal of Scientists) article, referring to the diagram in Figure 2.
Let A be the Sun, B Jupiter, C the first satellite entering the shadow of Jupiter and its exit at D, and let EFGHKL be the Earth placed at various distances from Jupiter.
Supposing that the Earth being at L, near the second quadrature, has seen the first satellite during its emergence or exit from the shadow at D and that 42.5 hours afterwards after one revolution of the satellite, Earth will find itself at K, and be seen returning to D. It is obvious that if the light takes time to traverse the interval LK, the satellite will be seen later returning in D that it would not be if the Earth remained at K, so that the revolution of this satellite, thus observed by the emergences, would be delayed by as much time as the light would take to pass from L to K, and that on the contrary in the other quadrant FG, where the Earth approaches, goes in front of the light, the successions of the immersions will appear as shortened as much as those of the emergences will appear lengthened.
(Many thanks to Rosanne Bersten for much valuable assistance in translating from the original old French.)