Further refining the measurement of the speed of light
In the 2016 Summer Solstice edition of the newsletter, we looked at Ole Rømer and how unexpected inconsistencies in his measurements of Jupiter’s moon Io lead to the first reasonably accurate estimate of the speed of light. This edition we look at a lesser-known set of astronomical observations made 50 years after Rømer by the English priest and astronomer, James Bradley, which further refined the measurement of the speed of light.
Not the Parallax Bradley Was Looking For
Like Rømer, James Bradley was not performing his measurements with the express purpose of measuring the speed of light. He was, in fact, attempting to improve the accuracy of a series of observations by the famous polymath Robert Hooke using the principle of parallax in an attempt to measure the distances to the stars.
Parallax is the effect whereby the position or direction of an object appears to differ when viewed from different positions. The straight line distance between the two observation points, plus the bearings measured from the observation points to the object can then be used to calculate the distance from the observation points to the object. In astronomy, the two bearings are the elevation of the star as it crosses the meridian (i.e. its declination), and the distance between the observation points is the diameter of the Earth’s orbit around the Sun. Shown below:
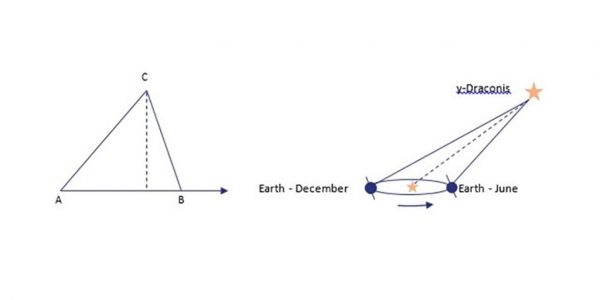
Bradley was attempting to measure the parallax of the star γ-Draconis (gamma Draconis, common name Etamin), a second magnitude star whose declination of +51°29′ meant that it passed almost exactly through the zenith point over London (whose latitude is 51°30’N). The main advantage of measuring the star near zenith is that it eliminated errors in measurement due to refraction from the Earth’s atmosphere. To measure the star’s position Bradley used a specialised and highly accurate instrument called a zenith sector telescope. This was mounted on an inside wall of a building, with the 24-foot optical tube passing through the roof via a chimney. The telescope was adjustable along the north-south meridian only, and the observer, lying on a couch, could move the telescope to observe the target star. The declination of the star could be read from a Vernier scale near the eyepiece. A picture of the instrument in situ is shown in Figure 2. In November 1725, the telescope was set up in the house of Bradley’s friend Samuel Molineux, and in December 1725, the observations of γ-Draconis began.

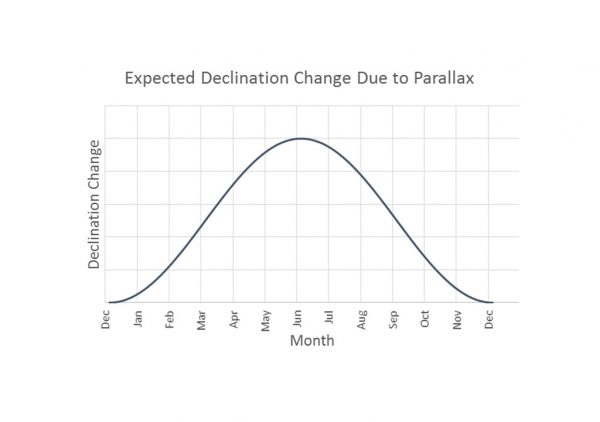
If γ-Draconis were close enough to measure a parallax, what would Bradley have expected to observe? In December, γ-Draconis passes over the North-South meridian at midday. As the Earth moves in its orbit, we would expect γ-Draconis to cross the meridian at an increasing northerly direction, reaching the northernmost point six months later in June, where it crosses the meridian at midnight. Furthermore, as the Earth moves back to its starting point the following December, γ-Draconis should appear to cross the meridian in an increasingly southerly direction, back to its starting point.
Today we know that γ-Draconis is 154 light-years from Earth, which produces a parallax of about 21 milliarcseconds, or about 6 × 10^5 degrees. This is like an observer in Perth measuring the height of a person standing in Sydney. Thus with hindsight, we can see that Bradley’s measurements were not going to be accurate enough to pick up any parallax. The first reliable stellar parallax measurements would have to wait for Friedrich Bessel in 1838, and today the most reliable parallax data was gathered by the Hipparcos satellite in the early 1990s.
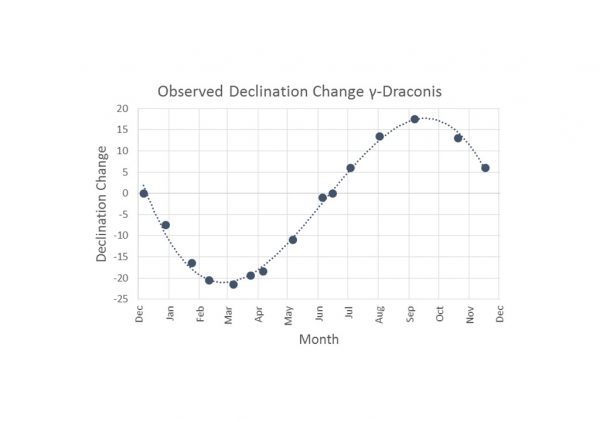
However, Bradley actually did observe a change in elevation at which γ-Draconis crossed the meridian, but the variation throughout the year was quite different to that expected with parallax described above. From December to March, γ-Draconis moved progressively south down the meridian, ultimately by 20″ from the starting position. From March to June, it moved back north to its starting point. Then from June to September, it continued northward until ultimately reaching 20″ north of the starting position, and finally, from September to December it headed back south to where it started (see Figure 3). Bradley had observed something new and unexpected.
 |
 |
Aberrant Thoughts
Bradley now had to find an explanation of the unexpected results. He checked the telescope for problems, repeated the observations and ruled out other phenomena such as notation (wobbling of the Earth’s axis of rotation). The (probably apocryphal) story goes that the answer came to him whilst sailing on the Thames, where he noticed that the tell-tale flag on the mast maintained its direction in a constant wind, even if the boat changed course.
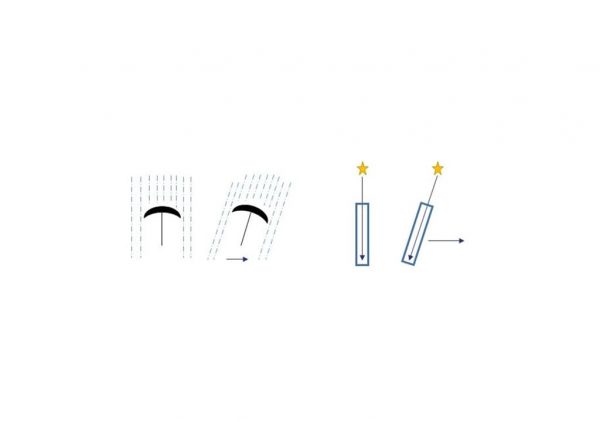
His final conclusion, which he sent to the Royal Society in 1729, was that the motion of the Earth (and thus his telescope) caused the light coming from γ-Draconis to appear to originate from a different point. He named these phenomena The Aberration of Light. An explanation of this effect is shown in Figure 4. Standing in a vertical downpour of rain, we hold the umbrella vertically. If, however, we start running, the rain appears to come in at an angle determined by the speed at which we are moving and the speed of the rain and the umbrella has to be tilted forward to block the rain. The situation for light coming from a star is very similar. When stationary with respect to the zenith star, our zenith telescope points vertically. However, if the Earth is moving with respect to the star, we must tilt our zenith scope ahead of the star’s true position in order to view it. In this case, the angle depends on the velocity of the Earth with respect to the star and the speed of light. Thus if we know the angle of the incoming light and the velocity of the Earth orbiting the Sun, we can work out the speed of light!
In 1729, Bradley wrote to the Royal Society about his observations of γ-Draconis, his theory of aberration to explain the results and thus the velocity of light his observations implied:
…it would follow, that Light moves, or is propagated as far as from the Sun to the Earth in 8′ 12″.
Using modern values for the radius of the Earth’s orbit, Bradley’s estimate equates to 301,000 km/s, within 1% of the currently accepted value of 299, 792 km/s.
Bradley’s discovery of the aberration of light, along with his later work on the nutation of the Earth’s axis are fundamental concepts in astronomy and were described by the French astronomer Jean-Baptiste Joseph Delambre as “the most brilliant and useful of the century.”
References
A Letter from the Reverend Mr. James Bradley Savilian Professor of Astronomy at Oxford, and F.R.S. to Dr.Edmond Halley Astronomer. Reg. &c. Giving an Account of a New Discovered Motion of the Fix’d Stars. (Phil. Trans January 1, 1729).